Các dạng bài tập định luật bảo toàn cơ năng

Định luật bảo toàn cơ năng là một trong những định luật cơ bản và quan trọng nhất trong vật lý, được ứng dụng rộng rãi để giải quyết các bài toán cơ học. Việc nắm vững Các Dạng Bài Tập định Luật Bảo Toàn Cơ Năng sẽ giúp bạn có cái nhìn tổng quan và phương pháp tiếp cận hiệu quả cho từng dạng bài cụ thể.

Phân loại các dạng bài tập định luật bảo toàn cơ năng

Dựa trên đặc điểm của vật thể và hệ vật được nhắc đến trong bài toán, ta có thể phân loại các dạng bài tập định luật bảo toàn cơ năng như sau:

## Dạng 1: Vật chuyển động chỉ dưới tác dụng của trọng lực

A ball is thrown vertically upward. As it rises, its kinetic energy decreases while its potential energy increases. At the highest point, the ball momentarily stops, and all its kinetic energy is converted into potential energy.

Đây là dạng bài tập cơ bản nhất, khi bỏ qua mọi lực cản, vật chỉ chịu tác dụng của trọng lực. Trong trường hợp này, cơ năng của vật được bảo toàn, nghĩa là tổng động năng và thế năng của vật ở vị trí bất kỳ là không đổi.

Ví dụ: Một quả bóng được ném thẳng đứng lên cao với vận tốc ban đầu là v. Bỏ qua sức cản không khí, hãy xác định:

• Độ cao cực đại mà quả bóng đạt được.
• Vận tốc của quả bóng khi nó trở về vị trí ban đầu.

Bài giải:

• Chọn mốc thế năng tại vị trí ném quả bóng.
• Tại vị trí ném, cơ năng của quả bóng là: W₁ = 1/2mv²
• Tại vị trí cao nhất, vận tốc của quả bóng bằng 0, cơ năng của quả bóng là: W₂ = mgh_max
• Áp dụng định luật bảo toàn cơ năng: W₁ = W₂ => h_max = v²/2g
• Tương tự, ta có thể chứng minh được vận tốc của quả bóng khi trở về vị trí ban đầu cũng là v.

## Dạng 2: Vật chuyển động có ma sát

A block slides down an inclined plane with friction. As it slides, some of its mechanical energy is converted into heat due to the frictional force acting on it.

Trong thực tế, bên cạnh trọng lực, vật luôn chịu tác dụng của lực ma sát. Lực ma sát là lực cản trở chuyển động, làm giảm cơ năng của vật. Phần cơ năng bị mất đi chuyển hóa thành nhiệt năng.

Ví dụ: Một vật khối lượng m trượt không vận tốc đầu từ đỉnh mặt phẳng nghiêng góc α và có hệ số ma sát trượt μ. Hãy tìm vận tốc của vật khi nó trượt đến chân mặt phẳng nghiêng.

Bài giải:

• Chọn mốc thế năng tại chân mặt phẳng nghiêng.
• Cơ năng của vật ở đỉnh mặt phẳng nghiêng: W₁ = mgh = mgl.sinα
• Cơ năng của vật ở chân mặt phẳng nghiêng: W₂ = 1/2mv²
• Công của lực ma sát: A_ms = -μmgcosα.l
• Áp dụng định luật bảo toàn cơ năng: W₂ – W₁ = A_ms => v = √(2gl(sinα-μcosα))

## Dạng 3: Vật chuyển động ném ngang

A projectile is launched horizontally from a height. As it travels through the air, it follows a parabolic trajectory. At any point during its flight, the sum of its kinetic energy and potential energy remains constant.

Đối với vật bị ném ngang, ta cần xét đến cả hai thành phần vận tốc theo phương ngang và phương thẳng đứng. Cơ năng của vật được bảo toàn trong suốt quá trình chuyển động.

Ví dụ: Một vật được ném ngang từ độ cao h so với mặt đất với vận tốc ban đầu v₀. Bỏ qua sức cản của không khí, hãy xác định:

• Thời gian vật rơi đến mặt đất.
• Tầm xa của vật.
• Vận tốc của vật ngay trước khi chạm đất.

Bài giải:

• Chọn hệ trục tọa độ Oxy, gốc O tại vị trí ném, Ox theo phương ngang, Oy theo phương thẳng đứng hướng xuống.
• Thời gian vật rơi đến mặt đất: t = √(2h/g)
• Tầm xa của vật: L = v₀.t = v₀.√(2h/g)
• Vận tốc của vật ngay trước khi chạm đất: v = √(v_x² + v_y²) = √(v₀² + 2gh)

## Dạng 4: Vật chuyển động trong trường lực đàn hồi

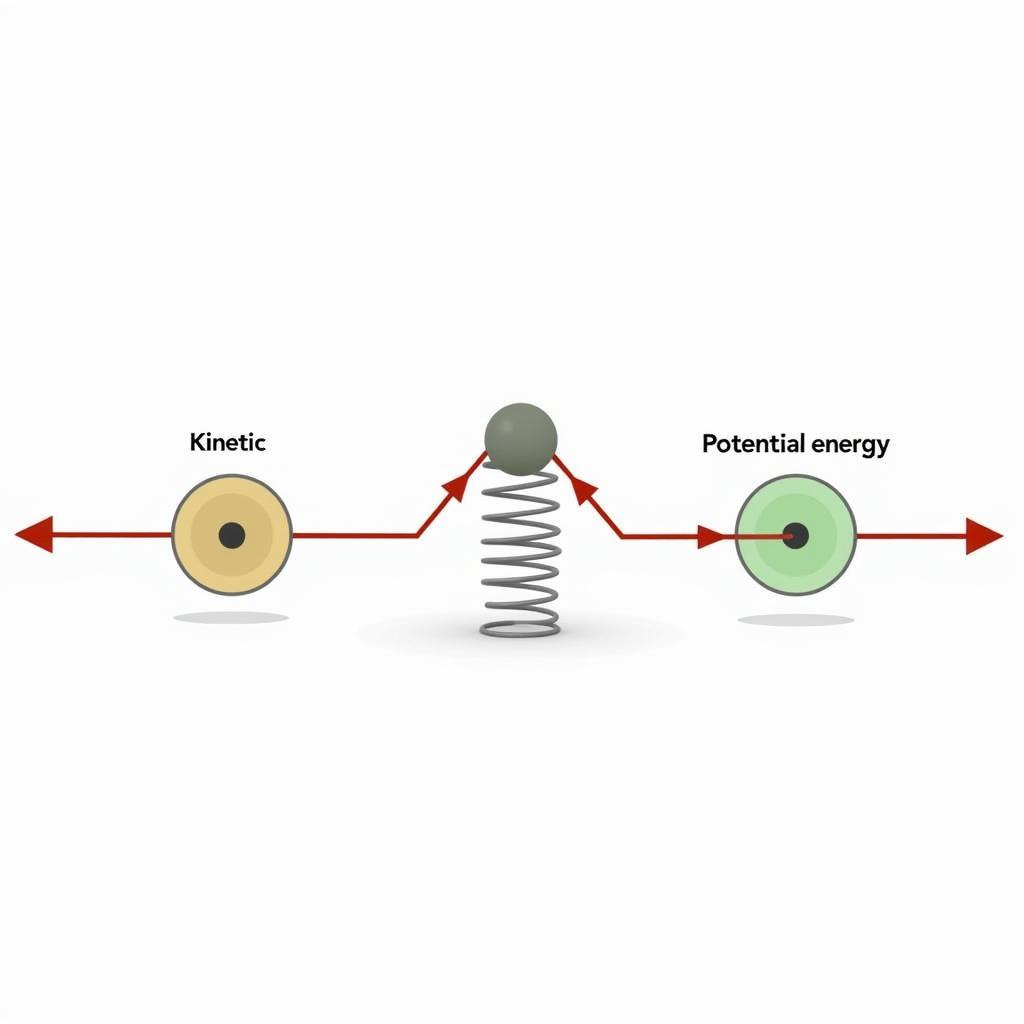A mass attached to a spring oscillates back and forth. As the mass moves, its kinetic energy and potential energy continuously interchange, but their sum remains constant.

Lực đàn hồi là lực phục hồi, có xu hướng đưa vật về vị trí cân bằng. Cơ năng của vật chuyển động trong trường lực đàn hồi cũng được bảo toàn.

Ví dụ: Một lò xo có độ cứng k, một đầu được gắn cố định, đầu còn lại gắn với vật có khối lượng m. Kéo vật ra khỏi vị trí cân bằng một đoạn A rồi thả nhẹ. Bỏ qua ma sát, hãy xác định:

• Vận tốc của vật khi đi qua vị trí cân bằng.
• Vận tốc của vật khi nó đi qua vị trí có li độ x (0 < x < A).

Bài giải:

• Chọn mốc thế năng tại vị trí cân bằng của vật.
• Cơ năng của vật ở vị trí biên: W₁ = 1/2kA²
• Cơ năng của vật ở vị trí cân bằng: W₂ = 1/2mv²
• Áp dụng định luật bảo toàn cơ năng: W₁ = W₂ => v_max = A√(k/m)
• Cơ năng của vật ở vị trí có li độ x: W₃ = 1/2kx² + 1/2mv²
• Áp dụng định luật bảo toàn cơ năng: W₁ = W₃ => v = √(k/m(A² – x²))

## Dạng 5: Hệ nhiều vật

Đối với hệ nhiều vật, cơ năng của hệ được bảo toàn nếu bỏ qua ma sát và các lực cản khác.

Ví dụ: Hai vật có khối lượng m₁ và m₂ được nối với nhau bằng một sợi dây không dãn, khối lượng không đáng kể, vắt qua ròng ròng cố định. Ban đầu, vật m₁ ở độ cao h so với mặt đất. Bỏ qua ma sát và khối lượng của ròng ròng, hãy xác định:

• Gia tốc của hệ vật.
• Lực căng của dây.
• Vận tốc của vật m₁ ngay trước khi chạm đất.

Bài giải:

• Chọn chiều dương là chiều chuyển động của vật m₁, mốc thế năng tại mặt đất.
• Áp dụng định luật II Newton cho từng vật:
  • Vật 1: m₁g – T = m₁a
  • Vật 2: T – m₂g = m₂a
• Gia tốc của hệ vật: a = (m₁ – m₂)g / (m₁ + m₂)
• Lực căng của dây: T = 2m₁m₂g / (m₁ + m₂)
• Áp dụng định luật bảo toàn cơ năng cho hệ vật:
  • Cơ năng của hệ vật lúc đầu: W₁ = m₁gh
  • Cơ năng của hệ vật ngay trước khi m₁ chạm đất: W₂ = (m₁ + m₂)v² / 2
• Áp dụng định luật bảo toàn cơ năng: W₁ = W₂ => v = √(2ghm₁ / (m₁ + m₂))

Mẹo giải bài tập định luật bảo toàn cơ năng hiệu quả

Để giải quyết các bài tập định luật bảo toàn cơ năng một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:

• Xác định rõ hệ vật cần nghiên cứu và các lực tác dụng lên hệ vật.
• Chọn mốc thế năng phù hợp để đơn giản hóa bài toán.
• Áp dụng định luật bảo toàn cơ năng cho hai vị trí khác nhau của vật hoặc hệ vật.
• Kết hợp với các định luật khác như định luật II Newton, định luật động lượng,… để giải quyết bài toán.
• Luyện tập giải nhiều bài tập với mức độ khó tăng dần để nắm vững kiến thức và kỹ năng giải toán.

Kết luận

Các dạng bài tập định luật bảo toàn cơ năng rất đa dạng, từ cơ bản đến nâng cao. Nắm vững lý thuyết, phân loại bài tập và luyện tập thường xuyên là chìa khóa giúp bạn chinh phục dạng bài tập này một cách dễ dàng.

Bạn muốn tìm hiểu thêm về các dạng bài tập định luật bảo toàn cơ năng khác?

Hãy truy cập bài tập trắc nghiệm định luật bảo toàn cơ năng để thử sức với những câu hỏi thú vị và củng cố kiến thức của bạn!

Bạn cần sự hỗ trợ về pháp lý trong lĩnh vực game?

Hãy liên hệ ngay với Luật Game!

• Số điện thoại: 0903883922
• Email: [email protected]
• Địa chỉ: Đoàn Thị Điểm, An Lộc, Bình Long, Bình Phước, Việt Nam

Đội ngũ luật sư giàu kinh nghiệm của chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7!