Bài Tập Quy Luật Phân Phối Chuẩn

Quy luật phân phối chuẩn, hay còn gọi là phân phối Gauss, là một khái niệm quan trọng trong thống kê và xác suất. Bài Tập Quy Luật Phân Phối Chuẩn giúp người học nắm vững lý thuyết và áp dụng vào thực tế, từ việc tính toán xác suất đến phân tích dữ liệu. Xem ngay để hiểu rõ hơn về bài tập quy luật phân phối chuẩn và ứng dụng của nó. Sau đoạn mở đầu này, chúng ta sẽ cùng nhau khám phá sâu hơn về chủ đề này.

Hiểu Về Quy Luật Phân Phối Chuẩn

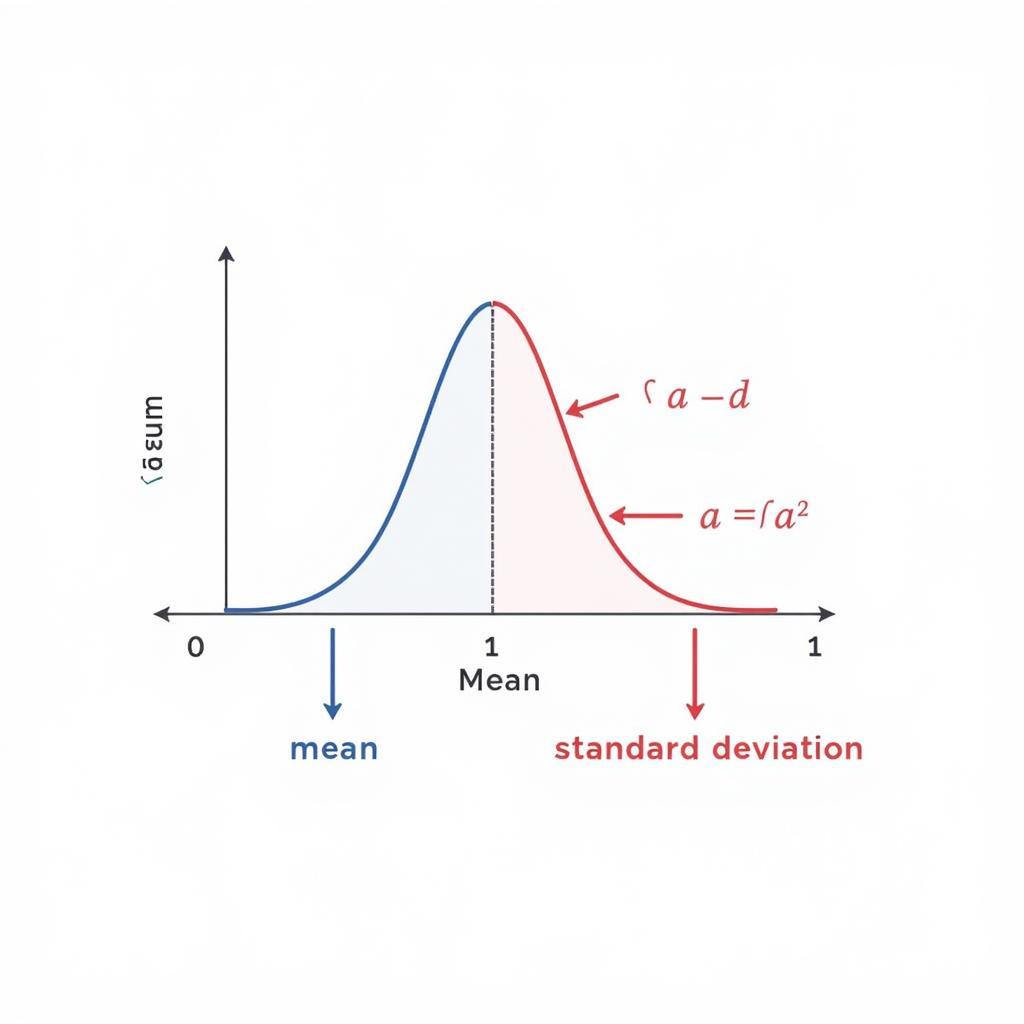
Quy luật phân phối chuẩn mô tả cách dữ liệu phân bố xung quanh giá trị trung bình. Đặc trưng bởi đồ thị hình chuông đối xứng, phân phối này cho thấy phần lớn dữ liệu tập trung gần giá trị trung bình, trong khi dữ liệu ở xa giá trị trung bình xuất hiện với tần suất thấp hơn. Việc hiểu rõ quy luật này là nền tảng cho việc giải quyết bài tập quy luật phân phối chuẩn. Xem thêm báo pháp luật tin tức mới nhất để biết thêm thông tin hữu ích.

Các Thông Số Quan Trọng Của Phân Phối Chuẩn

Hai thông số quan trọng nhất của phân phối chuẩn là giá trị trung bình (μ) và độ lệch chuẩn (σ). Giá trị trung bình đại diện cho tâm của phân phối, trong khi độ lệch chuẩn đo lường mức độ phân tán của dữ liệu xung quanh giá trị trung bình. Độ lệch chuẩn càng lớn, dữ liệu càng phân tán.

Bài Tập Quy Luật Phân Phối Chuẩn Cơ Bản

Bài tập quy luật phân phối chuẩn cơ bản thường yêu cầu tính xác suất của một biến ngẫu nhiên nằm trong một khoảng giá trị cho trước. Để giải quyết các bài tập này, chúng ta cần sử dụng bảng phân phối chuẩn chuẩn hóa (Z-table) hoặc máy tính.

Ví Dụ Bài Tập

Giả sử chiều cao của học sinh lớp 12 tuân theo quy luật phân phối chuẩn với giá trị trung bình 170cm và độ lệch chuẩn 5cm. Tính xác suất một học sinh được chọn ngẫu nhiên có chiều cao từ 165cm đến 175cm.

Để giải bài toán này, ta cần chuẩn hóa biến ngẫu nhiên chiều cao bằng cách trừ đi giá trị trung bình và chia cho độ lệch chuẩn. Sau đó, tra bảng Z-table để tìm xác suất tương ứng.

Ứng Dụng Của Bài Tập Quy Luật Phân Phối Chuẩn

Bài tập quy luật phân phối chuẩn không chỉ giúp củng cố kiến thức lý thuyết mà còn có ứng dụng rộng rãi trong thực tế, ví dụ như trong kiểm định giả thuyết, phân tích dữ liệu, và dự đoán. Tham khảo thêm thông tin về công ty luật gia phạm.

Bài Tập Quy Luật Phân Phối Chuẩn Nâng Cao

Bài tập nâng cao thường liên quan đến việc áp dụng quy luật phân phối chuẩn trong các tình huống phức tạp hơn, chẳng hạn như phân phối của tổng hoặc hiệu của các biến ngẫu nhiên.

Phân Phối Của Tổng Và Hiệu Các Biến Ngẫu Nhiên

Nếu X và Y là hai biến ngẫu nhiên độc lập tuân theo quy luật phân phối chuẩn, thì tổng và hiệu của chúng cũng tuân theo quy luật phân phối chuẩn. Điều này rất hữu ích trong việc phân tích dữ liệu và dự đoán. Xem thêm về bài báo cáo về luật môi trường trong doanh nhiệp để mở rộng kiến thức pháp luật.

Phân Phối Tổng Hiệu Biến Ngẫu Nhiên

Kết Luận

Bài tập quy luật phân phối chuẩn là một phần quan trọng trong việc học thống kê và xác suất. Việc nắm vững các khái niệm và phương pháp giải bài tập sẽ giúp bạn áp dụng quy luật này vào thực tế một cách hiệu quả. Bên cạnh việc học lý thuyết, việc thực hành thường xuyên là chìa khóa để thành công với bài tập quy luật phân phối chuẩn. Bạn có thể tìm hiểu thêm về coông ty việt luật.

Ứng Dụng Bài Tập Quy Luật Phân Phối Chuẩn

FAQ

1. Quy luật phân phối chuẩn là gì?
2. Làm thế nào để tính xác suất sử dụng bảng Z-table?
3. Độ lệch chuẩn ảnh hưởng đến phân phối chuẩn như thế nào?
4. Ứng dụng của quy luật phân phối chuẩn trong thực tế là gì?
5. Làm thế nào để giải bài tập quy luật phân phối chuẩn nâng cao?
6. Phân phối của tổng và hiệu các biến ngẫu nhiên tuân theo quy luật gì?
7. Tài liệu nào hữu ích cho việc học về quy luật phân phối chuẩn?

Mô tả các tình huống thường gặp câu hỏi.

Các câu hỏi thường gặp xoay quanh cách tính xác suất, cách sử dụng bảng phân phối chuẩn, và cách áp dụng quy luật phân phối chuẩn vào các tình huống thực tế.

Gợi ý các câu hỏi khác, bài viết khác có trong web.

Bạn có thể tìm hiểu thêm về các chủ đề liên quan như kiểm định giả thuyết, phân tích dữ liệu, và dự đoán trên trang web của chúng tôi. Xem thêm thông tin tại báo pháp luật trường mầm non nam tân.