Chứng Minh Định Luật De Morgan
Định luật De Morgan là một khái niệm quan trọng trong logic toán và đại số Boolean, được sử dụng rộng rãi trong khoa học máy tính, thiết kế mạch điện tử, và cả trong việc phân tích các hệ thống game phức tạp. Bài viết này sẽ hướng dẫn bạn chứng minh định luật de morgan một cách chi tiết và dễ hiểu.
Định luật De Morgan là gì?
Định luật De Morgan bao gồm hai mệnh đề mô tả mối quan hệ giữa phép phủ định, phép hợp và phép giao của các tập hợp hoặc mệnh đề logic. Nói một cách đơn giản, định luật này cho phép chúng ta chuyển đổi phép phủ định của một biểu thức logic phức tạp.
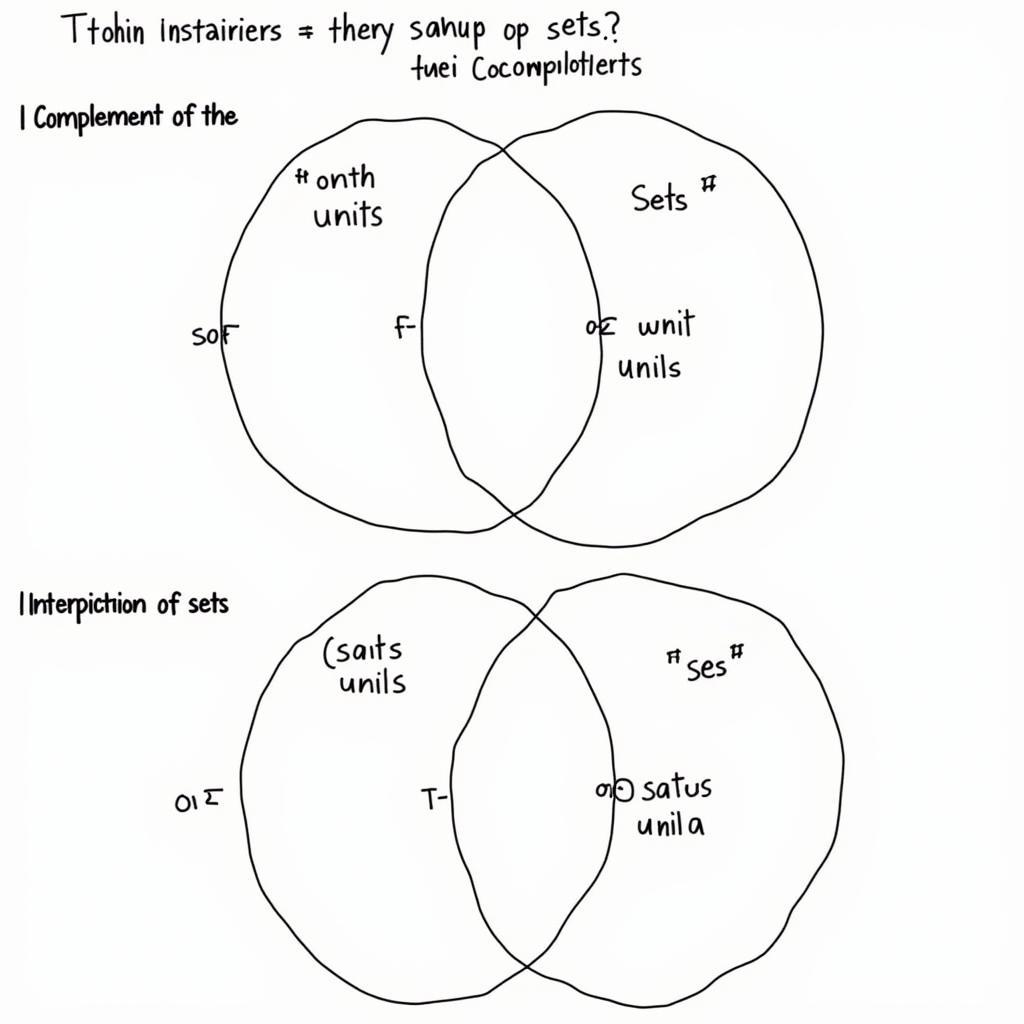
 Biểu đồ Venn minh họa định luật De Morgan
Biểu đồ Venn minh họa định luật De Morgan
Chứng minh Định luật De Morgan bằng bảng chân trị
Một cách phổ biến để chứng minh luật đối ngẫu de morgan là sử dụng bảng chân trị. Bảng chân trị liệt kê tất cả các giá trị có thể có của các mệnh đề thành phần và kết quả của biểu thức logic tương ứng.
Chứng minh mệnh đề thứ nhất: ¬(A ∨ B) ≡ ¬A ∧ ¬B
| A | B | A ∨ B | ¬(A ∨ B) | ¬A | ¬B | ¬A ∧ ¬B |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | T | F | F | T | F |
| F | T | T | F | T | F | F |
| F | F | F | T | T | T | T |
Như bạn có thể thấy, cột ¬(A ∨ B) và ¬A ∧ ¬B giống hệt nhau, chứng minh rằng hai biểu thức này tương đương.
Chứng minh mệnh đề thứ hai: ¬(A ∧ B) ≡ ¬A ∨ ¬B
| A | B | A ∧ B | ¬(A ∧ B) | ¬A | ¬B | ¬A ∨ ¬B |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | F | T | F | T | T |
| F | T | F | T | T | F | T |
| F | F | F | T | T | T | T |
Tương tự, cột ¬(A ∧ B) và ¬A ∨ ¬B giống nhau, chứng minh sự tương đương của hai biểu thức.
Ứng dụng của Định luật De Morgan trong Game
Định luật De Morgan có nhiều ứng dụng trong lập trình game, đặc biệt là trong việc tối ưu hóa logic và AI. Ví dụ, khi thiết kế hệ thống nhiệm vụ trong game, bạn có thể sử dụng định luật De Morgan để đơn giản hóa các điều kiện phức tạp.
Giả sử một nhiệm vụ yêu cầu người chơi phải hoàn thành cả nhiệm vụ A và nhiệm vụ B. Điều kiện để hoàn thành nhiệm vụ chính là A ∧ B. Nếu muốn kiểm tra xem người chơi chưa hoàn thành nhiệm vụ chính, ta có thể dùng ¬(A ∧ B). Áp dụng định luật De Morgan, ta có thể viết lại điều kiện này thành ¬A ∨ ¬B, nghĩa là người chơi chưa hoàn thành nhiệm vụ A hoặc chưa hoàn thành nhiệm vụ B.
“Việc nắm vững các luật logic toán rời rạc như định luật De Morgan là rất quan trọng đối với bất kỳ lập trình viên game nào. Nó cho phép chúng ta viết code hiệu quả và dễ bảo trì hơn.” – Ông Nguyễn Văn A, chuyên gia lập trình game tại VGame Studio.
Kết luận
Chứng Minh định Luật De Morgan không khó nếu bạn hiểu rõ các khái niệm cơ bản về logic toán. Định luật này là một công cụ mạnh mẽ giúp đơn giản hóa các biểu thức logic phức tạp và có nhiều ứng dụng thực tiễn trong lập trình game và các lĩnh vực khác. Hiểu rõ chứng minh định luật de morgan sẽ giúp bạn tối ưu hóa code và xây dựng các hệ thống logic phức tạp một cách hiệu quả hơn.
FAQ
- Định luật De Morgan được sử dụng trong lĩnh vực nào?
- Làm thế nào để chứng minh định luật De Morgan bằng phương pháp đại số?
- Có những biến thể nào khác của định luật De Morgan?
- Tại sao định luật De Morgan quan trọng trong lập trình game?
- Định luật De Morgan có liên quan gì đến nội dung quy luật giá trị?
- Tôi có thể tìm bài tập quy luật moocgan ở đâu?
- Làm thế nào để áp dụng định luật De Morgan vào thiết kế mạch điện tử?
Mô tả các tình huống thường gặp câu hỏi.
Người dùng thường tìm kiếm cách chứng minh định luật De Morgan khi họ đang học logic toán, đại số Boolean hoặc lập trình. Họ có thể gặp khó khăn trong việc hiểu cách thức hoạt động của định luật này và cách áp dụng nó vào các bài toán cụ thể.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các luật logic khác tại đây. Xem thêm bài viết về ứng dụng của logic toán trong game.




