Các Dạng Bài Tập Định Luật Kepler

Định luật Kepler là nền tảng cơ bản để hiểu về chuyển động của các hành tinh quanh Mặt Trời. Việc nắm vững các dạng bài tập định luật Kepler không chỉ giúp học sinh, sinh viên đạt điểm cao trong các kỳ thi mà còn mở ra cánh cửa khám phá vũ trụ bao la. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về các dạng bài tập thường gặp, cùng với những phương pháp giải quyết hiệu quả.

Các Dạng Bài Tập Định Luật Kepler Thường Gặp

Định luật Kepler bao gồm ba định luật miêu tả chuyển động của các hành tinh. Mỗi định luật lại dẫn đến các dạng bài tập khác nhau. Dưới đây là một số dạng bài tập phổ biến:

Bài tập liên quan đến định luật 1 (Định luật quỹ đạo): Xác định hình dạng quỹ đạo, tính toán các thông số của ellipse như bán trục lớn, bán trục nhỏ, tâm sai.
Bài tập liên quan đến định luật 2 (Định luật diện tích): Tính toán vận tốc của hành tinh tại các vị trí khác nhau trên quỹ đạo, so sánh tốc độ tại điểm cận nhật và điểm viễn nhật.
Bài tập liên quan đến định luật 3 (Định luật chu kỳ): So sánh chu kỳ và bán trục lớn của các hành tinh khác nhau, xác định chu kỳ quay của một hành tinh khi biết bán trục lớn.

Bài tập định luật Kepler về quỹ đạo

Phương Pháp Giải Bài Tập Định Luật Kepler

Để giải quyết các bài tập định luật Kepler, bạn cần nắm vững các công thức và hiểu rõ bản chất của từng định luật.

Đối với định luật 1: Cần nhớ rằng quỹ đạo của hành tinh là một ellipse, với Mặt Trời nằm tại một trong hai tiêu điểm.
Đối với định luật 2: Diện tích quét bởi vectơ bán kính nối Mặt Trời và hành tinh trong những khoảng thời gian bằng nhau là bằng nhau. Điều này cho phép tính toán vận tốc của hành tinh tại các vị trí khác nhau trên quỹ đạo.
Đối với định luật 3: Bình phương chu kỳ quay của hành tinh tỉ lệ với lập phương bán trục lớn của quỹ đạo. Công thức này cho phép so sánh chu kỳ và bán trục lớn của các hành tinh khác nhau.

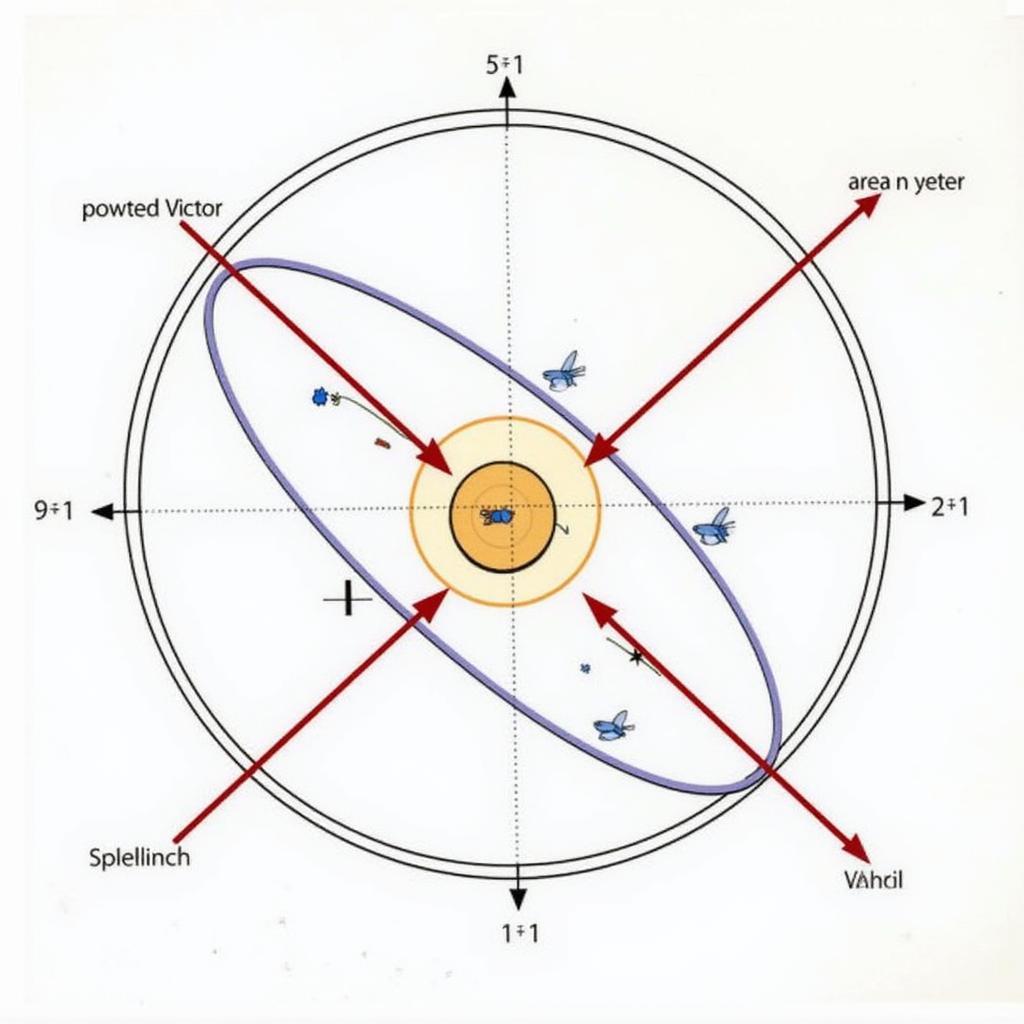Phương pháp giải bài tập định luật Kepler

Ví Dụ Bài Tập Định Luật Kepler

Một hành tinh có chu kỳ quay quanh Mặt Trời là T và bán trục lớn là a. Nếu bán trục lớn tăng gấp đôi, chu kỳ quay mới của hành tinh sẽ là bao nhiêu?

Giải:

Theo định luật 3 Kepler, ta có: T²/a³ = hằng số. Gọi T’ là chu kỳ mới khi bán trục lớn là 2a. Ta có: (T’)²/(2a)³ = T²/a³. Từ đó, ta tính được T’ = 2√2T.

“Hiểu rõ bản chất của ba định luật Kepler là chìa khóa để giải quyết mọi bài tập liên quan. Đừng chỉ học thuộc công thức mà hãy cố gắng hình dung và hiểu ý nghĩa vật lý đằng sau chúng.” – GS.TS Nguyễn Văn A, chuyên gia Vật lý Thiên văn.

Kết luận

Các dạng bài tập định luật Kepler rất đa dạng, từ việc xác định hình dạng quỹ đạo đến tính toán chu kỳ quay của hành tinh. Nắm vững các công thức và phương pháp giải quyết sẽ giúp bạn tự tin chinh phục mọi bài tập. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về các dạng bài tập định luật Kepler.

FAQ

Định luật Kepler áp dụng cho những loại thiên thể nào?
Làm thế nào để phân biệt giữa điểm cận nhật và điểm viễn nhật?
Định luật Kepler có áp dụng cho các vệ tinh nhân tạo không?
Ý nghĩa của hằng số trong định luật 3 Kepler là gì?
Làm thế nào để tính toán vận tốc của hành tinh tại một điểm bất kỳ trên quỹ đạo?
Có những phần mềm nào hỗ trợ giải bài tập định luật Kepler?
Định luật Kepler có liên quan gì đến luật vạn vật hấp dẫn của Newton?

Mô tả các tình huống thường gặp câu hỏi.

Học sinh thường gặp khó khăn trong việc áp dụng định luật 2 để tính toán vận tốc. Việc hình dung diện tích quét bởi vectơ bán kính có thể gây khó hiểu.

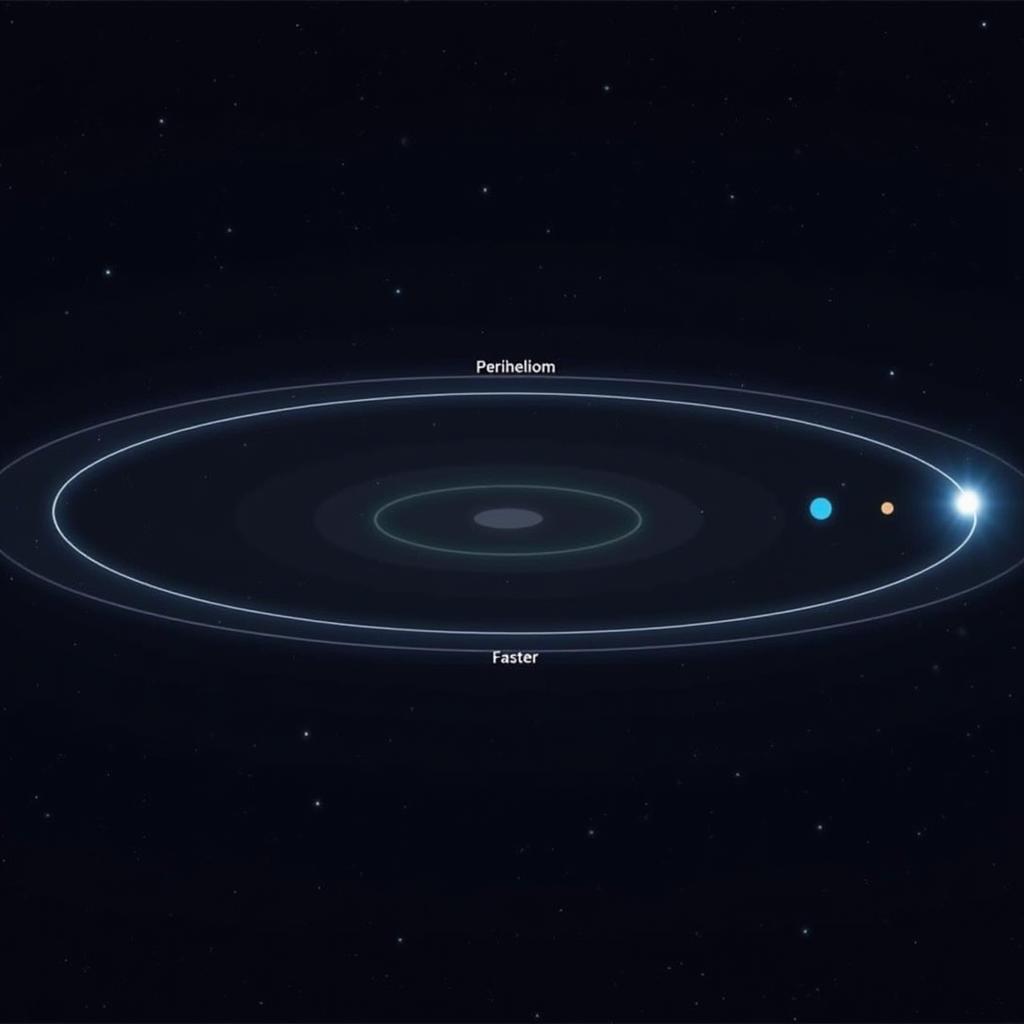Tính toán vận tốc hành tinh