Cách Giải Bì Tập Định Luật Bảo Toàn Cơ Năng

Định luật bảo toàn cơ năng là một trong những nguyên lý quan trọng nhất trong vật lý, việc nắm vững cách giải bài tập liên quan đến định luật này là chìa khóa để thành công trong môn học. Bài viết này sẽ hướng dẫn bạn Cách Giải Bì Tập định Luật Bảo Toàn Cơ Năng một cách chi tiết và hiệu quả.

Nắm Vững Lý Thuyết Định Luật Bảo Toàn Cơ Năng

Trước khi bắt đầu giải bài tập, việc hiểu rõ lý thuyết là điều kiện tiên quyết. Định luật bảo toàn cơ năng phát biểu rằng: “Trong một hệ kín, không có ma sát và các lực không thế, tổng cơ năng của hệ luôn được bảo toàn”. Cơ năng là tổng của động năng và thế năng. Động năng liên quan đến chuyển động, trong khi thế năng liên quan đến vị trí hoặc cấu hình của vật.

Các Bước Giải Bài Tập Định Luật Bảo Toàn Cơ Năng

Dưới đây là các bước cơ bản để giải quyết các bài toán về định luật bảo toàn cơ năng:

Xác định hệ kín: Đầu tiên, bạn cần xác định hệ nào được coi là kín. Một hệ kín là một hệ không trao đổi năng lượng với môi trường xung quanh.
Xác định các dạng năng lượng: Xác định xem hệ có những dạng năng lượng nào, ví dụ như động năng, thế năng trọng trường, thế năng đàn hồi.
Áp dụng định luật bảo toàn cơ năng: Viết phương trình bảo toàn cơ năng cho hệ. Phương trình này thường có dạng: W_đầu = W_sau, trong đó W là tổng cơ năng.
Giải phương trình: Giải phương trình để tìm các đại lượng chưa biết.

Phân Tích Bài Toàn Vật Rơi Tự Do

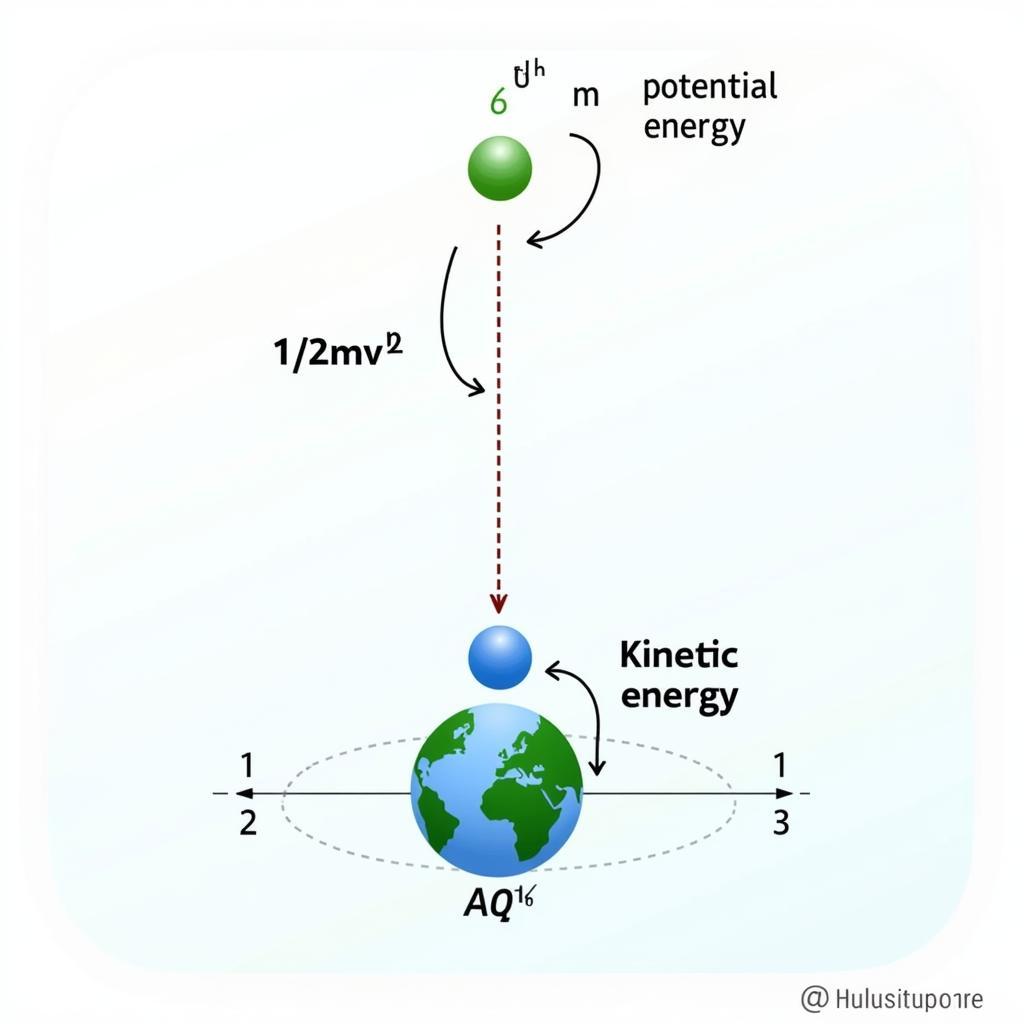
Một ví dụ điển hình về bài toán bảo toàn cơ năng là vật rơi tự do. Khi một vật rơi tự do, thế năng trọng trường của nó chuyển thành động năng.

Ví dụ Vật Rơi Tự Do

Một vật có khối lượng m rơi từ độ cao h. Tính vận tốc của vật khi chạm đất.

Xác định hệ kín: Hệ gồm vật và Trái Đất.
Xác định dạng năng lượng: Ban đầu vật có thế năng trọng trường mgh. Khi chạm đất, vật có động năng 1/2mv².
Áp dụng định luật: mgh = 1/2mv².
Giải phương trình: v = √(2gh).

Giải bài tập vật rơi tự do

Bài Toàn Con Lắc Đơn

Con lắc đơn cũng là một ví dụ thường gặp. Cơ năng của con lắc được bảo toàn khi bỏ qua ma sát.

Phân Tích Chuyển Động Con Lắc Đơn

Một con lắc đơn có chiều dài l, được thả từ vị trí lệch một góc θ so với phương thẳng đứng. Tính vận tốc của con lắc khi nó đi qua vị trí cân bằng.

Hệ kín: Con lắc và Trái Đất.
Dạng năng lượng: Thế năng trọng trường ở vị trí ban đầu và động năng ở vị trí cân bằng.
Định luật: mgl(1-cosθ) = 1/2mv².
Giải: v = √(2gl(1-cosθ)).

Giải bài tập con lắc đơn

Lời Khuyên Cho Việc Giải Bài Tập Định Luật Bảo Toàn Cơ Năng

Luôn xác định rõ hệ kín và các dạng năng lượng liên quan.
Vẽ hình minh họa để dễ dàng hình dung bài toán.
Chú ý đến đơn vị của các đại lượng.

Kết luận

Cách giải bì tập định luật bảo toàn cơ năng đòi hỏi sự hiểu biết vững chắc về lý thuyết và kỹ năng áp dụng vào các bài toán cụ thể. Bằng cách làm theo các bước hướng dẫn trên và luyện tập thường xuyên, bạn sẽ nắm vững được phương pháp giải quyết các bài toán liên quan đến định luật bảo toàn cơ năng.

FAQ

Định luật bảo toàn cơ năng áp dụng được trong trường hợp nào?
Thế nào là một hệ kín?
Động năng và thế năng là gì?
Làm thế nào để xác định các dạng năng lượng trong một hệ?
Khi nào có thể bỏ qua ma sát trong bài toán?
Có những dạng bài tập nào thường gặp về định luật bảo toàn cơ năng?
Làm sao để phân biệt giữa động năng và thế năng?

Mô tả các tình huống thường gặp câu hỏi.

Các câu hỏi thường gặp xoay quanh việc xác định hệ kín, phân biệt các loại năng lượng và áp dụng công thức định luật bảo toàn cơ năng vào các bài toán cụ thể như vật rơi tự do, con lắc, lò xo…

Gợi ý các câu hỏi khác, bài viết khác có trong web.

Bạn có thể tìm hiểu thêm về các bài viết liên quan đến định luật bảo toàn năng lượng, động lượng, các dạng năng lượng khác… trên website của chúng tôi.